Kapitel 2 Procenter, indekstal og regneregler
2.1 Procentregneregler
2.1.1 Video procentregning
2.1.2 Video Excel basisvideo.
Procent betyder hundrededele, vi angiver procent med symbolet %.
Har man 200 kr. er 1% af 200 kr., altså en hundrededel af 200 kr. dvs. \[\frac{200\ kr.}{100} = 2\ kr.\]
Af de 200 kr. er 100% af 200 kr., altså hundrede hundrededele af 200 kr. dvs. \[\frac{200\ kr.}{100} \cdot 100 = 200\ kr.\] altså hele beløbet.
Af de 200 kr. er 40% af 200 kr., altså hundrede hundrededele af 200 kr. dvs. \[\frac{200\ kr.}{100} \cdot 40 = 80\ kr.\]
Af de 200 kr. er 120% af 200 kr., altså hundrede hundrededele af 200 kr. dvs. \[\frac{200\ kr.}{100} \cdot 120 = 240\ kr.\]
Vi dividerer altså med 100, når vi skal finde 1 %, og ganger med antallet af procent vi skal bestemme.
Hvor mange procent udgør 10 kr. af 100 kr.?
Dette kan vi finde ud af ved at bestemme andelen af 10 kr. ud af 100 kr., og derefter gange med 100:
\[\frac{10}{100} \cdot 100\% = 10\%\]
Hvor mange procent udgør 20 kr. af 400 kr.?
\[\frac{20}{400} \cdot 100\% = 5\%\]
Hvad er 50 + 10%
\[50 + \frac{50}{100} \cdot 10 = 55\]
Eller mere generelt og lidt nemmere, de 50 kr. er 100% + 10% er 110%, når vi omskriver dette til decimaltal får vi \(\frac{110\%}{100} = 1,1\)
Dvs. vi kan finde 50 + 10% som \(50 \cdot 1,1 = 55\)
Tilsvarende kan vi hurtigt finde 50 kr. - 10% som 100%-10%=90%=0.9
\[50*0.9 = 45\]
Et beløb er faldet fra 400 kr. til 250 kr. Hvor mange % er beløbet faldet?
\[\frac{400 - 250}{400} \cdot 100\% = 37.5\%\]
Efter at have lagt momsen 25% til et beløb, er beløbet vokset til 1000 kr. hvad var beløbet før vi lagde 25% til. Det betyder vi har lagt 25% til det ukendte beløb X, altså ganget det med 1.25.
Her kan vi tænke på udregningen som en ligning, dvs. et udsagn der skal være sandt.
\[X \cdot 1.25 = 1000\ kr.\]
Vi skal nu bestemme/isolere X, ved at dividere med 1.25 på begge sider:
\[\frac{X \cdot 1.25}{1.25} = 1000\ kr.\frac{1}{1.25} \rightarrow X = 1000\ kr.\ \cdot 0.8 \rightarrow X = 800\ kr.\]
Vi kan når man skal finde et beløb uden moms 25%, gange med \(\frac{1}{1.25} = 0.8\)
2.2 Indekstal
Tal omregnes til indekstal, ved at lade indekstallene være procentværdier i forhold til en bestemt værdi kaldet basis der har indeks 100.
\[Indeks = \frac{Væ\ \ rdi}{\text{basis}} \cdot 100\]
Hvis fx en aktie er steget fra kurs 133 til kurs 180, kan vi indeksere ved at sætte kurs 133 til basis og bestemme, den indekserede værdi af den nye kurs 180.
\[Indeks = \frac{180}{133} \cdot 100 = 135.34\]
Dette er smart hvis vi skal sammenligne, hvordan forskellige værdier udvikler sig over tiden.
2.2.0.1 Danske Bank og Jyske Bank
I figuren herunder kan vi se kursudviklingen for Danske Bank og Jyske Bank. Det er lidt svært at overskue med både åbne- lukkekurs osv.
Vi trækker nu kun lukkekursen hver måned ud for nogle måneder tilbage. Herunder har vi de de seneste justerede slutkurser for Danske Bank og Jyske Bank på månedsbasis.
Vi kan bedre sammenligne udviklingerne i aktiekursen ved at indeksere kurserne for de to banker.
Her ses den indekseredde kursudvikling grafisk:
Hvordan kommer man fra indekstal til det oprindelige beløb, når Danske Bank aktien i har kurs 190.51 2018-01-01, hvad er da kursen 2018-02-01 når indeks er 101.11?
Nu kan man opstille en ligning for beregning af indekstal, med en ubekendt værdi kursen 2018-02-01 nemlig:
\[\frac{X}{190.51}*100 = 101.11 \rightarrow X = 101.11*\frac{190.51}{100} \rightarrow X = 192.63\]
Det betyder kursen 2018-02-01 vil være 192.63.
2.3 Procentpoint
Procentpoint angiver hvor meget ændringen er i indekstallene. Hvis fx en indekseret kurs er ændret fra 110 til 130 er ændringen: 130-110=20 procentpoint. Vi kan udregne den procentvise ændring som:
\(\frac{130 - 110}{110} \cdot 100 = 18,18\%\)
Modtager en kandidat til kommunalvalget 4% af stemmerne, mod 2% forrige periode, er stigningen 2 procentpoint. Stigningen i procent er imidlertid:
\[\frac{4 - 2}{2} \cdot 100 = 100\%\]
Vi kan undersøge hvor meget ændringen i procentpoint i forhold til perioden før har været, ved indeks nu minus indeks for perioden tidligere.
2.4 Reduktionsregneregler
2.4.1 Video regnearternes hieraki.
Når a, b og c d er reelle tal gælder:
\[a + b = b + a\]
\[2 + 4 = 4 + 2\]
\[a + (b + c) = (a + b) + c = a + b + c\]
\[3 + \left( 4 + 5 \right) = \left( 3 + 4 \right) + 5 = 3 + 4 + 5 = 12\]
\[a + \left( b + c - d \right) = a + b + c - d\]
\[3 + \left( 4 + 5 - 6 \right) = 3 + 4 + 5 - 6 = 6\]
Husk reglen om at ændre fortegn på alle led når man hæver en negativ parentes.
\[a - ( b + c - d ) = a - b - c + d\]
\[3 - ( 4 + 5 - 6 ) = 3 - 4 - 5 + 6 = 0\]
\[a \cdot b\ = b \cdot a\ \]
\[3 \cdot 4 = 4 \cdot 3 = 12\]
\[a \cdot \left( b \cdot c \right) = \left( a \cdot b \right) \cdot c\ = a \cdot b \cdot c\ \]
\[3 \cdot \left( 4 \cdot 5 \right) = \left( 3 \cdot 4 \right) \cdot 5 = 3 \cdot 4 \cdot 5 = 60\]
\[a \cdot \left( b + c \right) = a \cdot b + a \cdot c\ \]
\[3 \cdot \left( 4 + 5 \right) = 3 \cdot 4 + 3 \cdot 5 = 27\]
Bemærk faktoren skal ganges på alle led i parentesen
\[a \cdot \left( b - c \right) = a \cdot b - a \cdot c\ \]
\[3 \cdot \left( 4 - 5 \right) = 3 \cdot 4 - 3 \cdot 5 = - 3\]
\[\left( a + b \right) \cdot \left( c + d \right) = a \cdot \left( c + d \right) + b \cdot (c + d) = a \cdot c + a \cdot d + b \cdot c + b \cdot d\ \]
\[\left( 3 + 4 \right) \cdot \left( 5 + 6 \right) = 3 \cdot 5 + 3 \cdot 6 + 4 \cdot 5 + 4 \cdot 6\]
\[\left( a + b \right)^{2} = \left( a + b \right) \cdot \left( a + b \right) = a^{2} + b^{2} + 2ab\]
\[\left( 2x + 3y \right)^{2} = 4x^{2} + 9y^{2} + 12xy\]
Kvadratet af en toleddet størrelse, er kvadratet på første led + kvadratet på andet led plus det dobbelte produkt
\[\left( a - b \right)^{2} = \left( a - b \right) \cdot \left( a - b \right) = a^{2} + b^{2} - 2ab\]
\[\left( 2x + 3y \right)^{2} = 4x^{2} + 9y^{2} + 12xy\]
Kvadratet af en toleddet størrelse, er kvadratet på første led + kvadratet på andet led minus det dobbelte produkt
\[\left( a + b \right) \cdot \left( a - b \right) = a^{2} - b^{2}\]
\[\left( 2x + 3y \right) \cdot \left( 2x - 3y \right) = 4x^{2} - 9y^{2}\]
2.5 Brøkregneregler
2.5.1 Video Brøkregneregler
En brøk består af en tæller øverst og en nævner nederst\(.\) Hvis man tænker på tælleren som hvor mange stykker lagkage der er, og nævneren som hvor store stykkerne er. En brøk repræsenterer det præcise tal man får ved at dividere tælleren med nævneren. \(\frac{1}{3}\) repræsenterer således \(1:3\), der udtrykt som decimalbrøk er ca. 0,6667, dette tal kan faktisk ikke skrives helt præcist som et decimaltal, så brøker er fine hvis man ønsker at beregne noget helt eksakt. Der gælder at hvis både tæller og nævner er et heltal \(\mathbb{Z}\), så er brøken et rationalt tal.
Man kan forlænge brøker ved at gange med samme tal i tæller og nævner:
\[\frac{a}{b} = \frac{a \cdot c}{b \cdot c}\]
Man kan forkorte brøker ved at dividere med samme tal i tæller og nævner, det er god stil når man rapporterer et brøktal som slutresultat, at dette er mest muligt forkortet:
\[\frac{a}{b} = \frac{\frac{a}{c}}{\frac{b}{c}}\]
Hvis 2 brøker har samme nævner kan man addere eller subtrahere dem direkte.
\[\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\]
\[\frac{a}{c} - \frac{b}{c} = \frac{a - b}{c}\]
Har 2 brøker ikke samme nævner, må man først skaffe fællesnævner ved at forlænge den ene eller begge. Er man i tvivl kan man altid forlænge begge brøker, med den anden brøks nævner således er man sikker på at de har fællesnævner.
\[\frac{a}{c} + \frac{b}{d} = \frac{a \cdot d}{c \cdot d} + \frac{b \cdot c}{c \cdot d} = \frac{a \cdot d + b \cdot c}{c \cdot d}\]
\[\frac{a}{c} - \frac{b}{d} = \frac{a \cdot d}{c \cdot d} - \frac{b \cdot c}{c \cdot d} = \frac{a \cdot d - b \cdot c}{c \cdot d}\]
Man ganger en brøk med et tal, ved at gange tallet med tælleren.
\[\frac{a}{b} \cdot c = \frac{a \cdot c}{b}\]
Brøk gange brøk er tæller gange tæller og nævner gange nævner.
\[\frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d}\]
Man dividerer en brøk med et tal, ved at gange tallet ind i nævneren.
\[\frac{a}{b}:c = \frac{a}{b \cdot c}\]
Man dividerer et tal med en brøk, ved at gange tallet med den omvendte brøk.
\[c:\frac{a}{b} = \frac{c \cdot b}{a}\]
Man dividerer en brøk med en anden, ved at gange den første med den omvendte brøk.
\[\frac{a}{b}:\frac{c}{d} = \frac{a \cdot d}{b \cdot c}\]
2.6 Potensregneregler
2.6.1 Video potensregneregler
Lad a, b være reelle tal og m og n naturlige tal, der gælder følgende regler for potensregneregler.
\[a^{n} \cdot a^{m} = a^{n + m}\]
\[3^{2} \cdot 3^{4} = 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 = 3^{6}\]
\[\frac{a^{n}}{a^{m}} = a^{n - m}\]
\[\frac{3^{4}}{3^{2}} = \frac{3 \cdot 3 \cdot 3 \cdot 3}{3 \cdot 3} = 3 \cdot 3 = 3^{2}\]
\[a^{n^{m}} = a^{n \cdot m}\]
\[4^{2^{3}} = 4^{2} \cdot 4^{2} \cdot 4^{2} = 4^{2 \cdot 3}\]
\[a^{n} \cdot b^{n} = \left( a \cdot b \right)^{n}\]
\[4^{3} \cdot 7^{3} = 4 \cdot 4 \cdot 4 \cdot 7 \cdot 7 \cdot 7 = 4 \cdot 7 \cdot 4 \cdot 7 \cdot 4 \cdot 7 = 28^{3} = \left( 4 \cdot 7 \right)^{3}\]
\[\frac{a^{n}}{b^{n}} = \left( \frac{a}{b} \right)^{n}\]
\[\frac{3^{3}}{4^{3}} = \frac{3 \cdot 3 \cdot 3}{4 \cdot 4 \cdot 4} = \frac{3}{4} \cdot \frac{3}{4} \cdot \frac{3}{4} = \left( \frac{3}{4} \right)^{3}\]
\[\frac{1}{a^{n}} = a^{- n}\]
\[\frac{1}{4^{3}} = \frac{4^{0}}{4^{3}} = 4^{0 - 3} = 4^{- 3}\]
\[a^{0} = 1\]
\[37^{0} = 1\]
Resultatet af kvadratroden af 16, \(\sqrt{16}\), er det tal der gange med sig selv giver 16
\[\sqrt{16} \cdot \sqrt{16} = 16 = 4 \cdot 4\]
dvs.
\[\sqrt{16} = 4\]
Bemærk her noget helt fantastisk!
\[\sqrt{16} \cdot \sqrt{16} = 16 = 16^{1} = 16^{\frac{1}{2} + \frac{1}{2}} = 16^{\frac{1}{2}} \cdot 16^{\frac{1}{2}}\]
Vi kan altså skrive \(\sqrt{16}\) som \(16^{\frac{1}{2}}\)
Tilsvarende betyder f.eks. 4 roden af 256, \(\sqrt[4]{256}\), at man skal finde det tal der gange med sig selv 4 gange giver 256.
\[\sqrt[4]{256} = 4\]
Fordi
\[4 \cdot 4 \cdot 4 \cdot 4 = 256\]
Det kan vi skrive som
\[\sqrt[4]{256} = 256^{\frac{1}{4}}\]
Husk et par nyttige regler eksemplificeret nedenfor:
\[\frac{1}{x} = x^{- 1}\]
\[\frac{1}{x^{17}} = x^{- 17}\]
\[\sqrt{x} = \sqrt[2]{x} = x^{\frac{1}{2}}\]
\[\sqrt[7]{x^{3}} = x^{\frac{3}{7}}\]
\[x^{0} = 1\]
\[2 \cdot \sqrt{2} = \sqrt{2} \cdot \sqrt{2} \cdot \sqrt{2} = \sqrt{8}\]
2.7 Løsning af ligninger
2.7.1 Video Løsning af ligninger
2.7.2 Video Løsning af uligheder
Vi har følgende regneregler for ligninger:
Man må addere og subtrahere med en konstant c, når man gør det på både højre og venstresiden.
\[a = b \Leftrightarrow a + c = b + c\]
\[a = b \Leftrightarrow a - c = b - c\]
Man må multiplicere og dividere med en konstant c forskellig fra 0, f.eks:
\[a = b \Leftrightarrow a*c = b*c\]
\[a = b \Leftrightarrow \frac{a}{c} = \frac{b}{c}\]
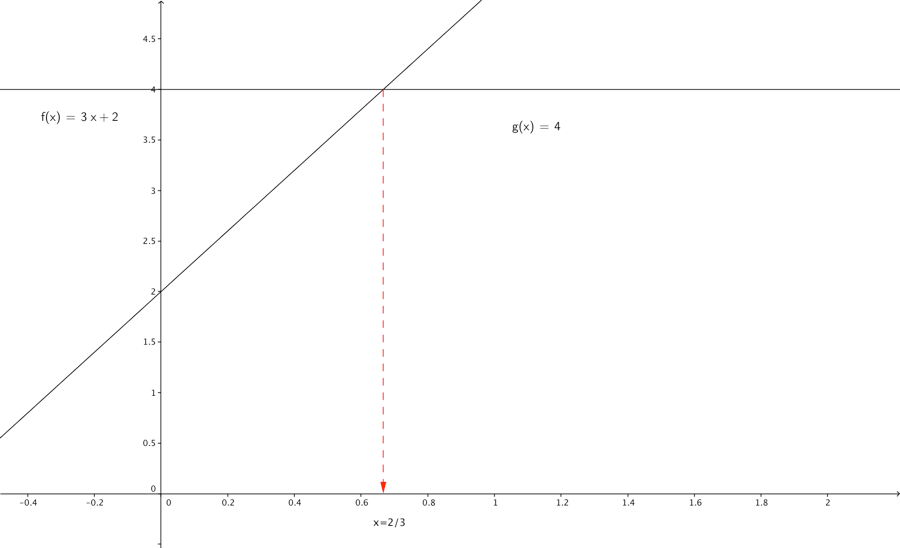
At løse en ligning betyder: bestem de variabelværdier for hvilken ligningen er sand, vi kalder mængden af disse værdier løsningsmængden L. Hvis vi betragter 1. Grads ligningen:
\[3x + 2 = 4\]
Her tilhører x=3 f.eks. ikke løsningsmængden L. for
\[3*3 + 2 \neq 4\]
Man kan hurtigt bestemme løsningsmængden ved at isolere x.
\[3x + 2 = 4 \Leftrightarrow\]
\[3x + 2 - 2 = 4 - 2 \Leftrightarrow\]
\[3x = 2 \Leftrightarrow\]
\[\frac{3x}{3} = \frac{2}{3} \Leftrightarrow\]
\[x = \frac{2}{3}\Leftrightarrow\]
\[L = \{\frac{2}{3}\}\]
Du kan bruge Wolframalpha til at tjekke dit resultat, indsæt 3x + 2 = 4 nedenfor og tryk enter, så løser Wolframalpha ligningen for dig. Du kan se hvorledes du gør dette ved at klikke her.
Der findes specialtilfælde af ligninger hvor L = Ø dvs. ingen løsning.
\[{5x = 7 + 5x}\Leftrightarrow{0x = 7}\Leftrightarrow{\ L = Ø}\]
Da der ikke findes x-værdier der kan gøre ligningen 0x=7 sand, siger vi løsningsmængden er Ø eller tom. Wolframalpha skriver “no solutions exist.”
Der findes også ligninger der er sande ligegyldigt hvilken værdi x har, så skriver vi:
\(L\mathbb{= R}\)
\[{5x + 3 = 7 + 5x - 4}\Leftrightarrow{0x = 0}\Leftrightarrow{\text{L}=\mathbb{R}}\]
Man kan måske få en bedre forståelse ved at løse 1. Gradsligningen, ved at indtegne hhv. højre- og venstreside som funktioner i et koordinatsystem.
