Kapitel 3 Funktioner og ligninger

3.1 Lineære funktioner

3.1.1 Video funktioner

3.1.2 Video Geogebra hjælpeprogram til funktioner

Man kan med fordel benytte fx. Geogebra til at tegne og arbejde med funktioner.

3.2 Generel Forskift liniær funktion

En funktion er et redskab, der beskriver sammenhængen mellem en uafhængig variabel x og en afhængig variabel y = f(x). Formen for en lineær funktionsforskrift skrives som:

$$f\left(x\right)=ax+b$$

$$hvora,b\in R$$

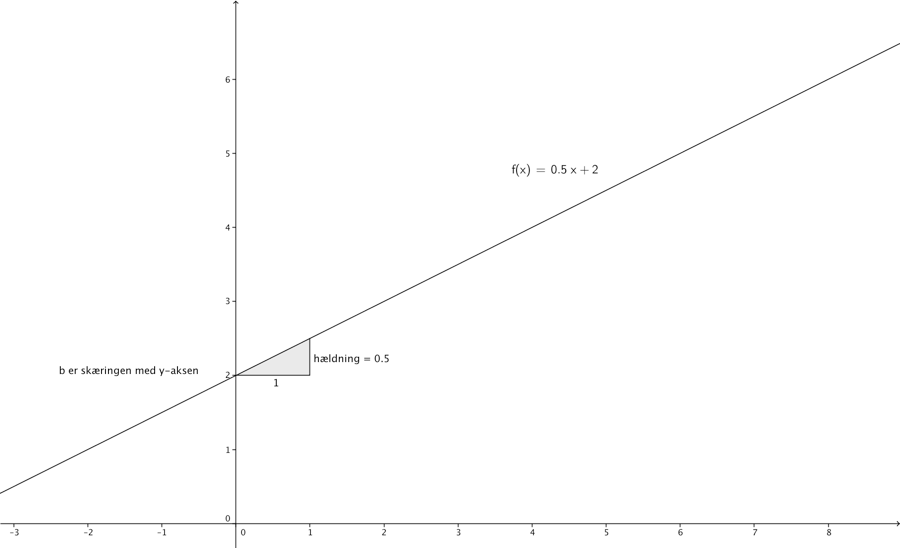
Vi kalder a for hældningskoefficienten, dette tal fortæller hvor meget y ændrer sig når x vokser med 1. Det vil sige hvor meget ændres funktionsværdien, når vi går en til højre på x-aksen. b er skæringen med y-aksen. Punktet hvor linjen skærer y-aksen har altid første-koordinat 0, dvs. punktet hedder (0,b).

På figuren ovenfor er $f\left(x\right)=0,5x+2$ tegnet ind. Her ses som nævnt, at linjen skærer y-aksen i (0,2), og hældningskoefficienten er 0,5.

Når man indsætter en x-værdi i funktionsforskriften får man funktionsværdien eller y-værdien. F.eks. vil x=2 give en y-værdi $f\left(2\right)=0,5\cdot 2+2=3$, det betyder punktet $(2,3)$ ligger på den rette linje.

En lineær funktion med positiv hældning $(hera=0,5)$ er en monotont voksende funktion, en sådan funktion ligner en bakke der går opad. Jo større a er des stejlere er bakken. En lineær funktion med negativ hældning, er en funktion der er monotont aftagende, det er en funktion der går nedad.

3.3 Bestemmelse af forskrift baseret på 2 punkter

Hvis vi kender 2 punkter $(x_1,y_1)og(x_2,y_2)$ på en ligning kan vi bestemme funktionsforskriften, $f\left(x\right)=ax+b$

$$a=\frac{y_1-y_2}{x_1-x_2}$$

$$b=y_1-a{x}_1$$

Hvorfor? Fordi vi kan skrive opskrive 2 ligninger med 2 ubekendte (a og b), når vi kender den generelle funktionsforskrift og de to punkter:

$$y_1=a{x}_1+b$$

$$y_2=a{x}_2+b$$

Se i senere afsnit hvordan man kan løse 2 ligninger med 2 ubekendte, her er de ubekendte jo a og b alle andre størrelser i ligningerne er kendte. Man kan så trække den ene ligning fra den anden, så forsvinder b, og man har en ligning med en ubekendt tilbage.

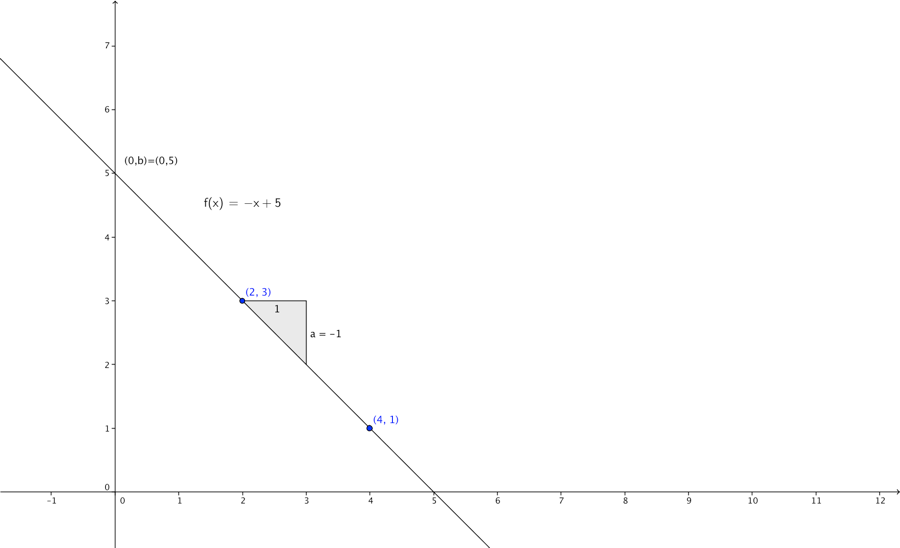
Hvis vi kender 2 punkter (2,3) og (4,1) på en lineær funktion og ønsker at bestemme forskriften, kan vi altså først finde a:

$$a=\frac{y_1-y_2}{x_1-x_2}=\frac{4-2}{1-3}=-\frac{2}{2}=-1$$

Bemærk det er ligegyldigt hvilket punkt man vælger som $(x_1,y_1)$ og $(x_2,y_2)$, men rækkefølgen i brøken, når man har valgt, er vigtig.

Man bestemmer nemt b, da det nu er den eneste ukendte i de 2 ligninger, behøver vi blot indsætte de øvrige kendte værdier i den ene ligning.

$$b=y_1-a{x}_1=3-(-1)\cdot 2=5$$

Så forskriften bliver altså

$$y=-x+5$$

Man kan også benytte www.wolframalpha.com her. til at bestemme linjen gennem 2 punkter. Skriv i feltet: line (2,3) and (4,1)

Det giver ligeledes forskriften for linjen. Man kan ligeledes benytte Wolfram til løsning af uligheder.

3.4 Selvtest lineære funktioner

Gå til selvtesten her.