Kapitel 4 2 ligninger med 2 ubekendte.
4.0.1 Video 2 ligninger med 2 ubekendte.
En ligning med 2 ubekendte kan f.eks. være:
\[3x = 2y + 6\]
Denne ligning kan vi omskrive til:
\[{y = 1\frac{1}{2}x - 3}\]
I koordinatsystemet vil denne ligning kunne afbilledes som nedenfor:
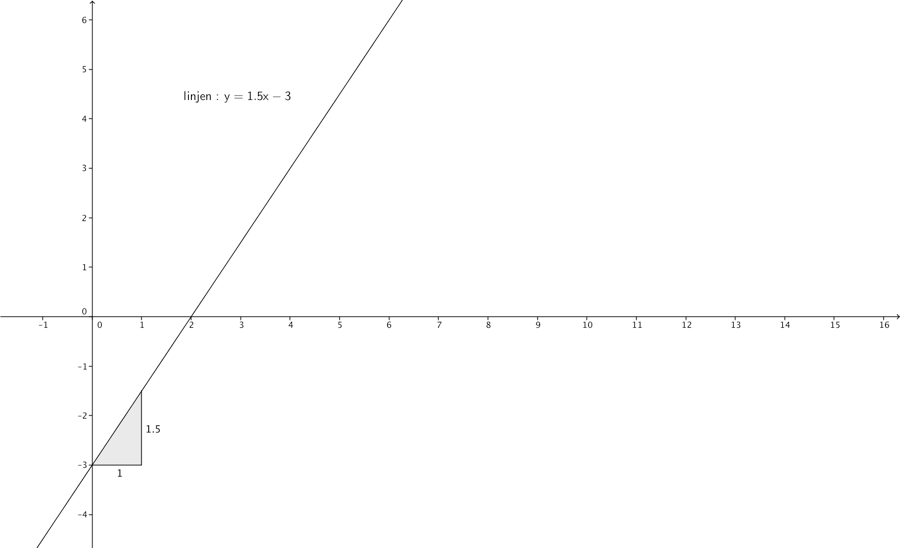
Hvis man skal løse 2 ligninger med 2 ubekendte, skal man gøre det samme, som når man løser en ligning med en ubekendt. Man skal altså finde de værdier af de 2 ubekendte der gør begge ligninger sande samtidigt. Vi kalder også 2 ligninger med 2 ubekendte for et ligningssystem. Sådanne ligninger med 2 ubekendte kan tegnes som rette linjer i et koordinatsystem, og derefter løses grafisk. Det betyder ikke noget at de ubekendte hedder noget andet end x og y, man navngiver dem blot som hhv. x og y. Hvis man tegner ligningerne med de 2 ubekendte ind i koordinatsystemet, er skæringspunktet mellem de to rette linjer, netop der hvor begge ligninger er sande.
Hvis vi f.eks. skal løse de 2 ligninger:
\[3x = 2y + 6\]
\[y = \frac{1}{2}x + 1\]
Kan vi omskrive dem dvs. isolere y’erne på venstresiden:
\[y = 1\frac{1}{2}x - 3\]
\[y = \frac{1}{2}x + 1\]
Og vi indtegner disse og finder skæringspunktet:
\[3x = 2y + 6\]
\[y = 2x + 1\]
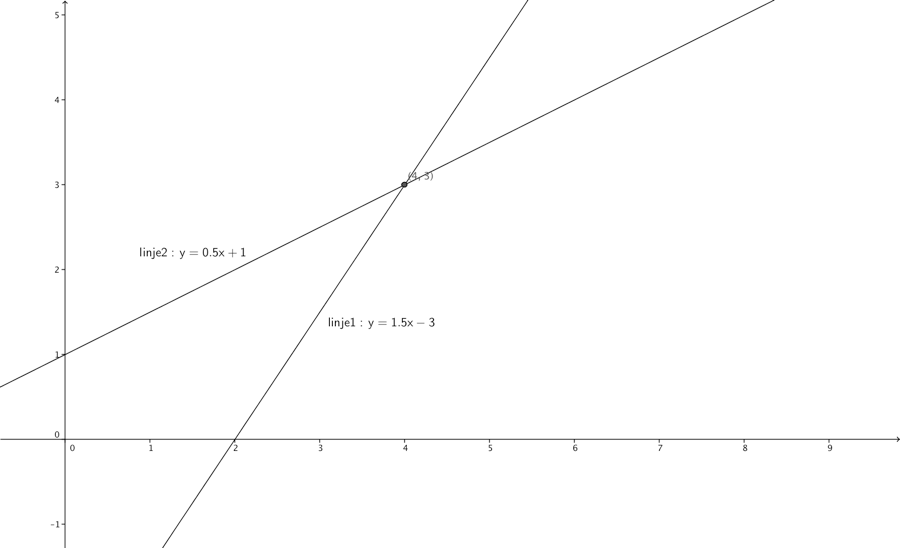
Ligesom med en ligning kan løsningsmængden være tom (hvis de 2 linjer de 2 ligninger danner er parallelle) eller \(\mathbb{R}^{2}\), (hvis ligningerne der dannes er identiske ). Men oftest vil linjerne skære hinanden.
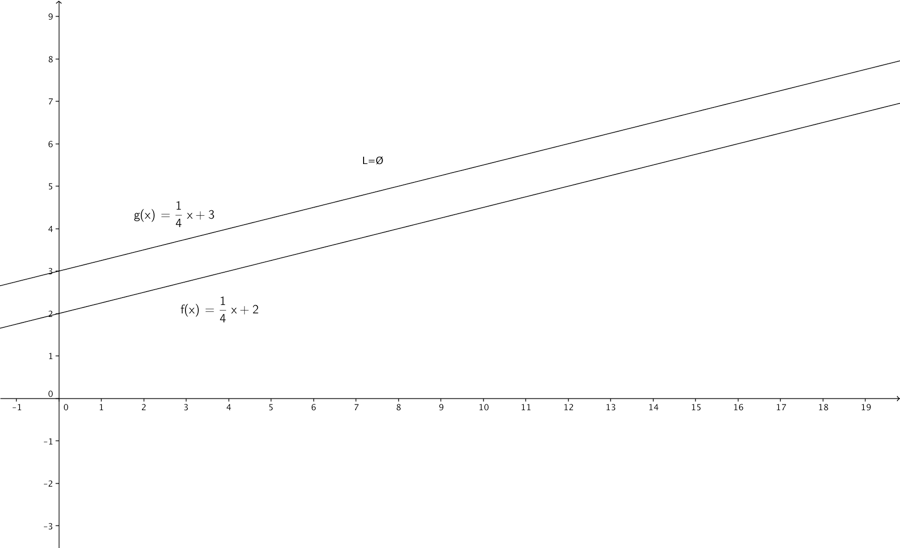
Der findes flere metoder til løsning af 2 ligninger med 2 ubekendte bl.a. substitutionsmetoden. Når vi benytter substitutionsmetoden, isolerer vi y i begge ligninger:
\[y = 1\frac{1}{2}x - 3\]
\[y = \frac{1}{2}x + 1\]
Vi ved at y i første og anden ligning skal have samme værdi når vi finder en løsning. Derfor ved vi også at venstresiderne skal være ens. Vi sætter så venstresiderne lig med hinanden og isolerer x:
\[1\frac{1}{2}x - 3 = \frac{1}{2}x + 1\]
\[1\frac{1}{2}x - \frac{1}{2}x = 3 + 1\]
\[x = 4\]
Vi ved nu at når x er lig med 4, har vi en løsning. Så kan vi bare indsætte x=4, i en af de oprindelige ligninger og finde værdien af y.
\[y = 1\frac{1}{2}x - 3\]
\[y = 1\frac{1}{2} \cdot 4 - 3\]
\[y = 3\]
og vi ser at vi får samme løsning som da vi benyttede den grafiske metode.
\[(4,3)\]
Vi kan ligeledes løse 2 ligninger med 2 ubekendte vha. wolfram. Skriv på https://www.wolframalpha.com: 3 x = 2 y + 6 and y = 1/2 x + 1
Så får vi skæringen (4,3)
Man kan løse ligningssystemer med flere end 2 ubekendte med matrix kommandoerne mmult og minverse i excel, men dette når vi ikke at gennemgå på dette kursus.
Vi bruger 2 ligninger med 2 ubekendte i mange økonomiske sammenhænge til fx. at finde den optimale mængde der skal afsættes for. Eller får at finde ligevægten på et marked som i eksemplet nedenfor.
4.1 Udbuds- og efterspørgselskurver
En vares prissætning er afgørende for hvor meget man kan afsætte af den pågældende vare. Jo højere pris desto færre varer kan man afsætte. Tilsvarende vil prissætningen være afgørende for, hvor meget producenterne vil udbyde, jo højere pris des flere varer udbydes. Vi forudsætter her at sammenhængen mellem pris og afsætning er lineær. Vi kan tegne efterspørgselskurver i et koordinatsystem med pris på y-aksen og afsætning på x-aksen. Dette er omvendt af hvordan vi normalt i matematik ville tegne en lineær funktion, idet vores forklarende variabel pris der styrer afsætningen er y.
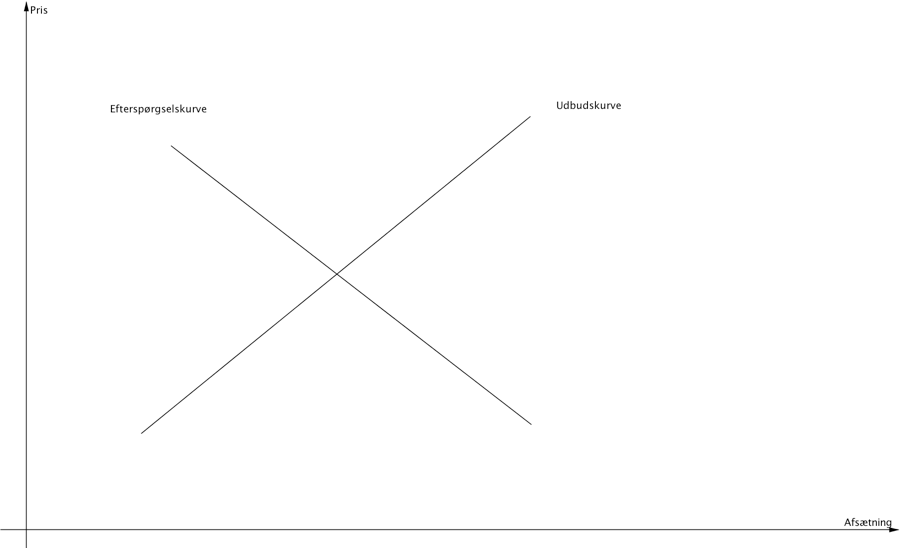
Efterspørgselskurven har negativ hældning og udbudskurven har positiv hældning.
Et marked er i ligevægt hvor udbuds- og efterspørgselskurven skærer hinanden.
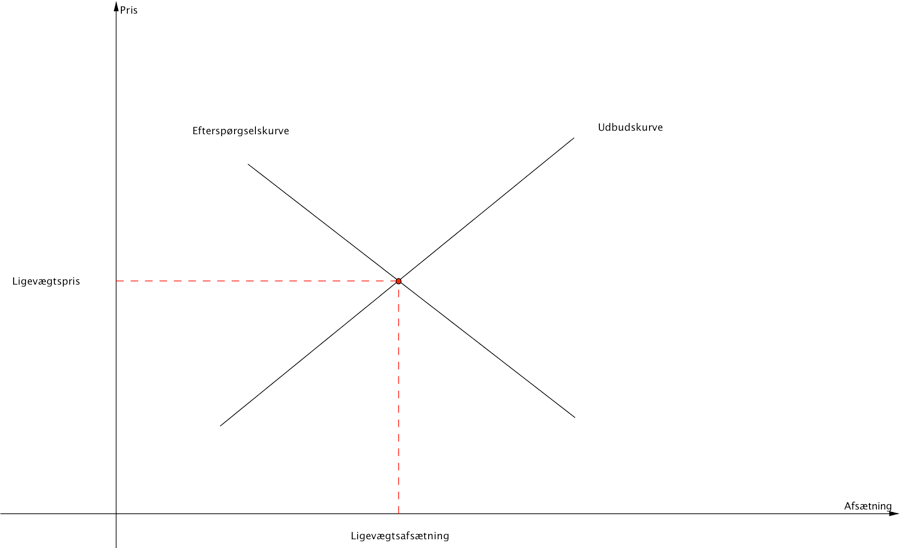
Hvordan finder vi ligevægtspris og afsætning?
Det gør vi ved substitutionsmetoden, som vi så tidligere.