Kapitel 7 Finansiel regning
7.0.1 Nutidsværdi og fremtidsværdi af en kapital
Vi benytter i finansiel regning vor viden fra eksponentielle funktioner, nedenstående eksempel viser hvordan sammenhængen er:
En kapital på K0 = 10.000 kr. sættes ind på en bankkonto, hvor der hvert år tilskrives en rente på 10%. Betegner vi kapitalens værdi efter 1 år med K1 , er denne:
K1 =10.000⋅1,10=11.000 kr.
da vi lægger 10 % til et tal ved at gange tallet med 1,10.
Efter 2 år er kapitalens værdi vokset til
K2 =11.000⋅1,10=12.100 kr.
og efter 3 år står der følgende beløb på bankkontoen
K3 =12.100⋅ 1,10=13.310 kr.
Der gælder altså at:
K1 =K0 ⋅ (1+r)
K2 =K1 ⋅ (1+r)
K3 =K2 ⋅ (1+r)
Osv.
Men dette kan vi skrive som:
K1 =K0 ⋅ (1+r)
K2 =K0 ⋅ (1+r)⋅(1+r)
K3 =K0 ⋅ (1+r)⋅(1+r)⋅(1+r)
Osv.
Eller vha. Potensregnereglerne:
K1 =K0 ⋅ (1+r)
K2 =K0 ⋅ (1+r)2
K3 =K0 ⋅ (1+r)3
.
.
.
Kn =K0 ⋅ (1+r)n
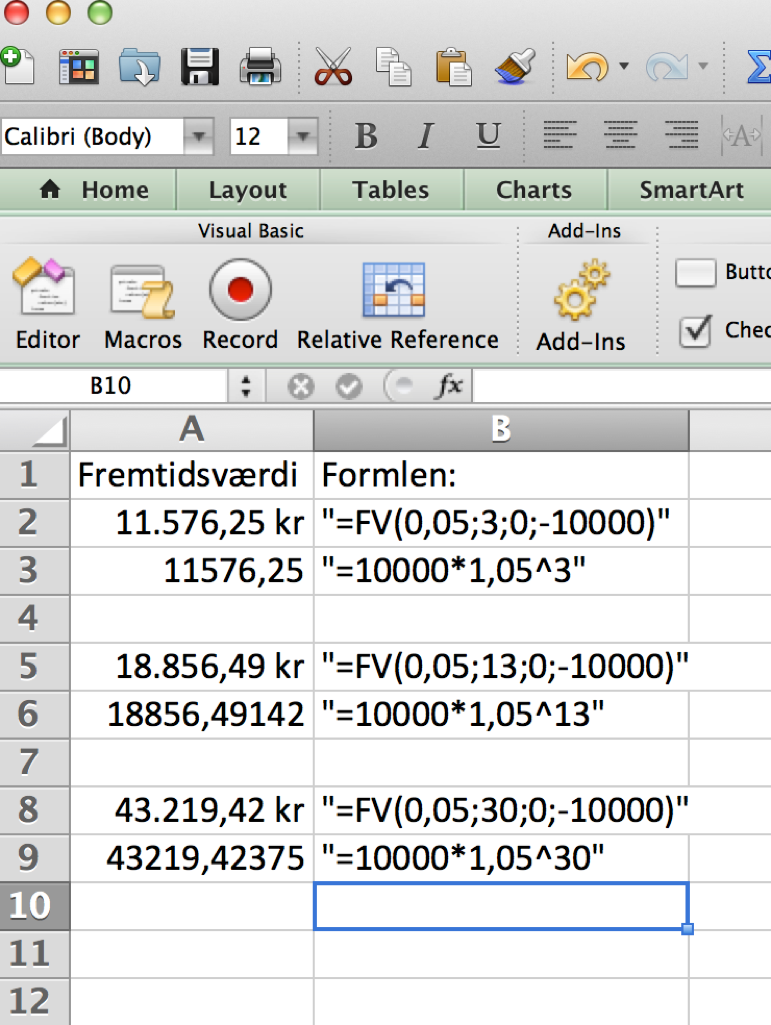
En mand sætter 10.000 ind på en konto med årlig rentetilskrivning 5%, hvad har han på kontoen efter 3, 13 og 30 år ?
\[K_{3} = 10.000 \cdot {1,05}^{3} = 11.576,25\]
\[K_{13} = 10.000 \cdot {1,05}^{13} = 18.856,49\]
\[K_{30} = 10.000 \cdot {1,05}^{30} = 43.219,42\]
I excel den engelske version, kan man enten skrive ovenstående formler ud, eller benytte fv kommandoen, fv betyder future value. I den danske version skriver man også fv for fremtidsværdi. I første søjle nedenfor står resultaterne, i anden søjle formlen i gåseøjne. Bemærk der er forskel på hvad man separerer argumenter med i forskellige excel-versioner, nogle versioner bruger komma “,” , andre versioner bruger semikolon “;” Man kan se hvad man skal bruge i den hjælpetekst der kommer op med gult.
De forskellige argumenter er:
FV(terminsrenten som decimaltal; antal terminer, ydelsen[^2]; nutidsværdi/pv/present value; type angiver man ikke da den står default korrekt)
I B2 cellen nedenfor står der derfor:
=FV(0,05;3;0;-10000)
Vi har altså 5% terminsrente, 3 terminer, ydelser 0 og -10.000,- i nutidsværdi. Bemærk excel angiver nutidsværdien med negativ værdi, man indsætter jo et beløb i dag, man kan tænke på det som man tager penge op af lommen i dag (derfor minus) og sætter dem ind på sin konto. Resultatet fremtidsværdien, bliver positivt, man angiver jo beløbet, man kan hæve og putte i lommen igen.
Vi kan opfatte fremtidsværdien Kn af en kapital K0 på et vilkårligt tidspunkt n ude i fremtiden som en funktion af antallet af år/terminer. Dvs. kapitalen er en konstant, (1+r) er en konstant.
Men potensen n er den variable.
Kn =K0 ⋅ (1+r)n
Kaldes fremskrivningsformlen, vi kalder
K0 kapitalen/ nutidsværdien/begyndelsesværdien
Kn fremtidsværdien
r renten/vækstraten
a = 1 + r fremskrivningsfaktoren/grundtallet
Vi har altså den generelle formel for fremtidsværdien af en kapital.
\[K_{n} = K_{0}\ \cdot \ \left( 1 + r \right)^{n}\]
Ved at isolere \(K_{0}\) får vi formlen for nutidsværdien af en kapital.
\[K_{0}\ = K_{n}\ \left( 1 + r \right)^{- n}\]
Tilsvarende kan vi isolere antallet af terminer vha. logaritmefunktionen ln.
\[K_{n} = K_{0}\ \cdot \ \left( 1 + r \right)^{n}\]
\[{\frac{K_{n}}{K_{0}} = \ \left( 1 + r \right)^{n}\ }\]
\[{\ln\left( \frac{K_{n}}{K_{0}} \right) = n \cdot \ln\left( 1 + r \right)}\]
\[{n = \frac{\ln\left( \frac{K_{n}}{K_{0}} \right)}{\ln\left( 1 + r \right)}\ }\]
Vi kan ligeledes isolere renten r.
\[K_{n} = K_{0}\ \cdot \ \left( 1 + r \right)^{n}\]
\[{\frac{K_{n}}{K_{0}} = \left( 1 + r \right)^{n}}\]
\[{\sqrt[n]{\frac{K_{n}}{K_{0}}} = 1 + r}\]
\[{r = \sqrt[n]{\frac{K_{n}}{K_{0}}} - 1}\]
7.1 Annuiteter
En annuitet er en række lige store betalinger/ydelser betalt ved starten af tidintervaller/terminer, af samme længde, renten er ens og tilskrives efter hver termin.
7.2 Fremtidsværdi af en annuitet
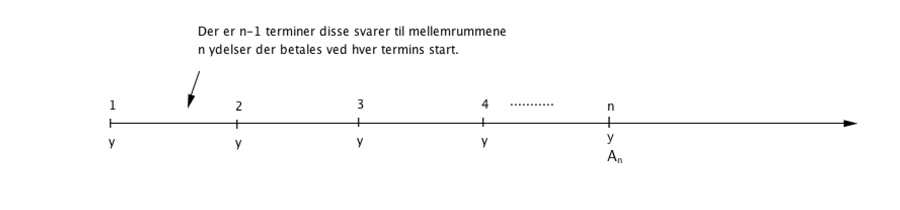
Hvis man indbetaler ydelsen y på en konto n gange til en fast terminsrente r, vil man kunne hæve \(A_{n}\), på tidspunkt n. Man kalder denne formel opsparingsformlen, fordi man sparer et beløb op det opsparede beløb på tidspunkt n er \(A_{n}\). Dette er illustreret på tidslinjen ovenfor, formlen for fremtidsværdien af annuiteten bliver:
\[A_{n} = y \cdot \frac{\left( 1 + r \right)^{n} - 1}{r}\]
En person indbetaler hvert halve år 1.000,- på en konto med halvårlig rentetilskrivning \(r = \ 0,02\), der foretages 10 indbetalinger, hvad er saldoen på kontoen efter sidste indbetaling.
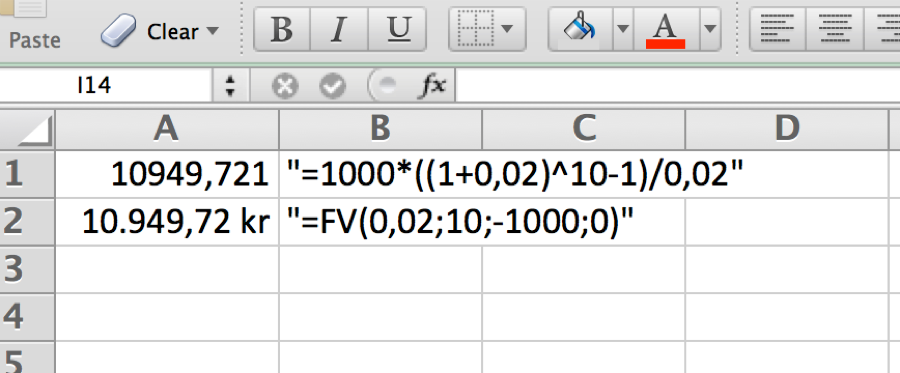
Her benytter vi i B2 cellen igen FV kommandoen. Bemærk ydelse/pmt argumentet der før var 0 er nu -1000, mens pv/nutidsværdi nu er 0. De -1000 er det beløb personen skal indbetale, i starten af hver termin.
Man kan komme ud for at man ikke kender en af de andre størrelser r, n eller y, men derimod kender \(A_{n}\). Hvis y eller n er ukendte, kan man udfra ovenstående formel isolere den ukendte størrelse ved reduktionsregnereglerne.
\[y = A_{n} \cdot \frac{r}{\left( 1 + r \right)^{n} - 1}\]
Excelformlen er PMT (YDELSE dansk version) denne bruger følgende argumenter
PMT(rate, nper, pv, fv, type), bemærk denne formel kan bruges til at finde ydelsen for både opsparings- og gældsformlen. Opsparingsformlens fv-værdi skal være 0.
Hvis man skal finde n, kan man isolere n i opsparingsformlen, man får da:
\[A_{n} = y \cdot \frac{\left( 1 + r \right)^{n} - 1}{r} \Leftrightarrow\]
\[n = \frac{\ln\left( \frac{A_{n} \cdot r}{y} + 1 \right)}{\ln\left( 1 + r \right)}\]
Eller bruge NPER(rate,pmt,pv,fv,type) funktionen i excel, her skal man huske at pv present value skal være 0. Hvis Öztürk ønsker at have $A_{n} =$15.000,- til rådighed, og kan betale terminsydelser på \(y = 500, -\) og terminsrenten er r=0,01, hvor mange ydelser skal der da betales.
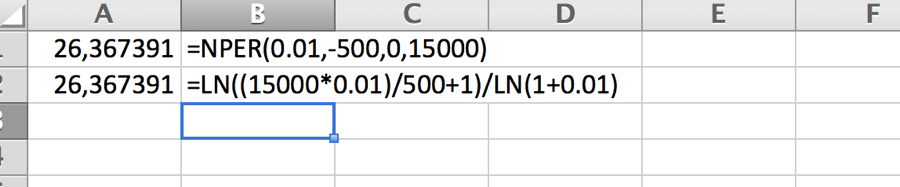
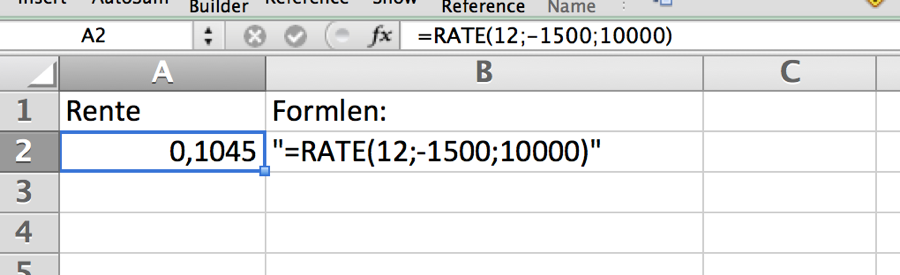
Hvis renten er ukendt kan vi ikke opskrive en entydig formel hvor r isoleres. Vi kan benytte excels RATE(nper,pmt,pv,fv,type,guess) funktion. Hvis Sørensen indsætter 2000 hvert 12 gange, og han lige efter sidste indsættelse har 25340,- på kontoen, har terminsrenten været:
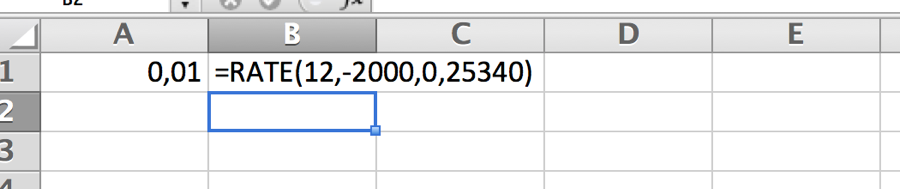
7.3 Nutidsværdi af en annuitet
Nutidsværdien af en annuitet fortæller os hvad en person kan låne på tidspunkt 0, hvis han i n terminer afdrager samme beløb y, og renten tilskrives terminsvis. Bemærk tidslinjen har tidpunkt 0 med, i modsætning til fremtidsværdien af en annuitet, det er på dette tidspunkt man låner beløbet \(A_{0}\). Man kalder formlen for nutidsværdien af en annuitet gældsformlen fordi, man stifter gæld på tidspunkt 0. Hvorfor starter man ikke ved 1 ligesom i forrige formel, det skyldes at når man ønsker at låne penge nu, låner man ikke penge man betaler tilbage med det samme, dem ville man jo så alligevel ikke have glæde af.
\[A_{0} = y \cdot \frac{1 - \left( 1 + r \right)^{- n}}{r}\]
Hvis en person kan afdrage y/pmt. kr. 1.000,- på et lån over n=10 terminer, og der på restgælden tilskrives en fast terminsrente r=0,02, ved begyndelsen af hver termin, kan han i alt låne kr. 8.982,50 kr nu. Den første linje i udskriften fra excel, viser hvordan formlen bruges. Den anden linje viser hvorledes den indbyggede excelfunktion beregner nutidsværdien, bemærk PV (present value) er den engelske formel den danske hedder NV (nutidsværdien).
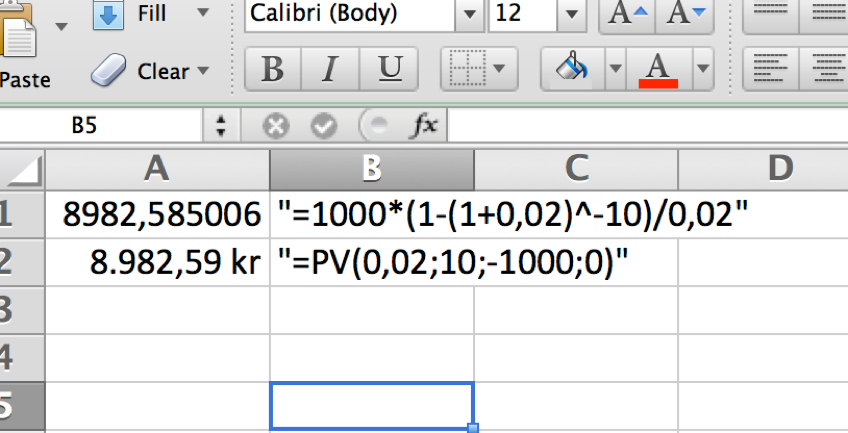
Der er en tæt sammenhæng mellem fremtids- og nutidsværdien af en annuitet. Nutidsværdien af annuiteten er fremtidsværdien \(A_{n}\) på tidspunkt n tilbagediskonteret til tidspunkt 0.
\[A_{n} \cdot \left( 1 + r \right)^{- n} = y \cdot \frac{\left( 1 + r \right)^{n} - 1}{r} \cdot \left( 1 + r \right)^{- n} = A_{0}\]
Tilsvarende er \(A_{0}\ \) fremskrevet til tidspunkt n ved at gange med faktoren \(\left( 1 + r \right)^{n}\) det samme som \(A_{n}\).
\[A_{0} \cdot \left( 1 + r \right)^{n} = y \cdot \frac{1 - \left( 1 + r \right)^{- n}}{r} \cdot \left( 1 + r \right)^{n} = A_{n}\]
Man kan komme ud for at man ikke kender en af de andre størrelser r, n eller y, men derimod kender \(A_{0}\). Hvis y eller n er ukendte, kan man ud fra ovenstående formel isolere den ukendte størrelse ved reduktionsregnereglerne. Er y ukendt får vi:
\[y = A_{0} \cdot \frac{r}{1 - \left( 1 + r \right)^{- n}}\]
Hvis Jensen gerne vil låne 20.000,- og kender terminsrenten 4%, og skal betale gælden af over 12 terminer, kan man vha. ovenstående formel beregne hans ydelse.
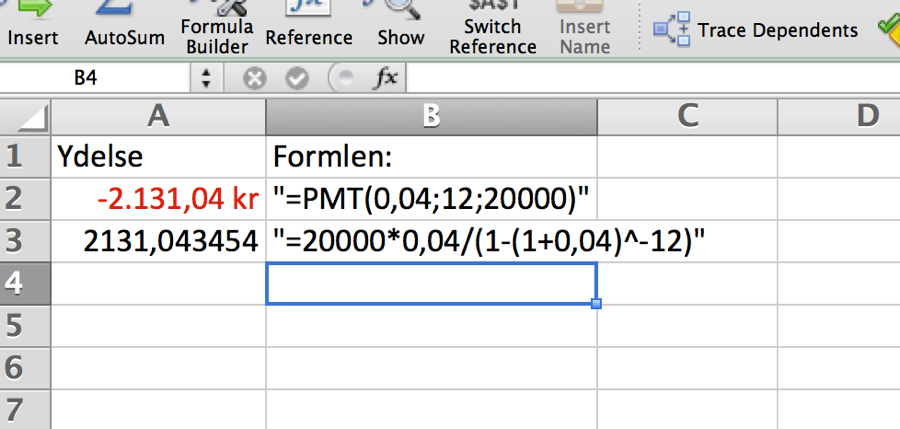
Er n antallet af ydelser ukendt kan vi omskrive formlen til
\[n = - \frac{\ln\left( 1 - \frac{\left( A_{0} \cdot r \right)}{y} \right)}{\ln\left( 1 + r \right)}\ \]
Hansen betaler 1.000,- i ydelse, på et lån på 10.000,- med en terminsrente på 3%, antallet af ydelser n bliver:
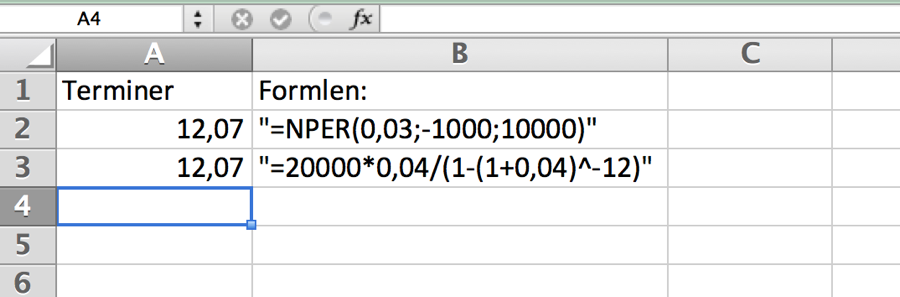
Hansen skal altså betale 13 ydelser, den sidste ydelse bliver mindre end de første 12.
Hvis der er ukendt terminsrente r, kan man ikke opstille et eksplicit udtryk for renten, ligningen bliver et polynomium af grad n. Der findes ikke altid en entydig løsning til et polynomium, hvorfor excel og anden software benytter en algoritme til at finde en løsning.
Hvis Larsen låner 10.000,- der afdrages ved 12 ydelser af 1.500,-, vil vi kunne benytte rate-kommandoen. Vi vil få en terminsrente på 10,45.
